FIFA for the GCSE Physics calculation win

Student: Did you know FIFA is also the name of a video game, Sir?

Me: Really?

Student: Yeah. It’s part of a series. I just got FIFA 20. It’s one of my favourite games ever.

Me: Goodness me. I had no idea. I just chose the letters ‘FIFA’ completely and utterly at random!

The FIFA method is an AQA mark scheme-friendly* way of approaching GCSE Physics calculation questions. (It is also useful for some Y12 Physics students.)

I mentioned it in a previous blog and @PedagogueSci was kind enough to give it a boost here, so I thought I’d explain the method in a separate blog post. (Update: you can also watch my talk at ChatPhysics Live 2021 here.)

The FIFA method:

1. Avoids the use of formula triangles
2. Minimises the cognitive load on students when approaching calculations.

Why we shouldn’t use formula triangles

Formula triangles are bad news. They are a cognitive dead end.

During a university admissions interview for veterinary medicine, I asked a prospective student to explain how they would make up a solution for infusion into a dog. Part of the answer required them to work out the volume required for a given amount and concentration. The candidate started off by drawing a triangle, then hesitated, eventually giving up in despair. […]

They are a trick that hides the maths: students don’t apply the skills they have previously learned. This means students don’t realise how important maths is for science.

I’m also concerned that if students can’t rearrange simple equations like the one above, they really can’t manage when equations become more complex.

— Jenny Koenig, Why Are Formula Triangles Bad? [Emphases added]

[Update: this 2016 article from Ed Southall also makes a very persuasive case against formula triangle.]

I believe the use of formula triangle also increases (rather than decreases) the cognitive load on students when carrying out calculations. For example, if the concentration c is 0.5 mol dm^-3 and the number of moles n required is 0.01 mol, then in order to calculate the volume V they need to:

• recall the relevant equation and what each symbol means and hold it in working memory
• recall the layout of symbols within the formula triangle and either (a) write it down or (b) hold it in working memory
• recall that n and c are known values and that V is the unknown value and hold this information in working memory when applying the formula triangle to the problem

The FIFA method in use (part 1)

The FIFA acronym stands for:

• FORMULA
• INSERT VALUES
• FINE TUNE (this often, but not always, equates to rearranging the formula)
• ANSWER

Lets look at applying it for a typical higher level GCSE Physics calculation question

We add the FIFA rubric:

Students have to recall the relevant equation as it is not given on the Data and Formula Sheet. They write it down. This is an important step as once it is written down they no longer have to hold it in their working memory.

Note that this is less cognitively demanding on the student’s working memory as they only have to recall the formula on its own; they do not have to recall the formula triangle associated with it.

Students find it encouraging that on many mark schemes, the selection of the correct equation may gain a mark, even if no further steps are taken.

Next, we insert the values. I find it useful to provide a framework for this such as:

We can ask general questions such as: “What data are in the question?” or more focused questions such as “Yes or no: are we told what the kinetic energy store is?” and follow up questions such as “What is the kinetic energy? What units do we use for that?” and so on.

Note that since we are considering each item of data individually and in a sequence determined by the written formula, this is much less cognitively demanding in terms of what needs to be held in the student’s working memory than the formula triangle method.

Note also that on many mark schemes, a mark is available for the correct substitution of values. Even if they were not able to proceed any further, they would still gain 2/5 marks. For many students, the notion of incremental gain in calculation questions needs to be pushed really hard otherwise they will not attempt these “scary” calculation questions.

Next we are going to “fine tune” what we have written down in order to calculate the final answer. In this instance, the “fine tuning” process equates to a simple algebraic rearrangement. However, it is useful to leave room for some “creative ambiguity” here as we can also use the “fine tuning” process to resolve difficulties with units. Tempting though it may seem, DON’T change FIFA to FIRA.

We fine tune in three distinct steps (see addendum):

Finally, we input the values on a calculator to give a final answer. Note that since AQA have declined to provide a unit on the final answer line, a mark is available for writing “kg” in the relevant space — a fact which students find surprising but strangely encouraging.

The key idea here is to be as positive and encouraging as possible. Even if all they can do is recall the formula and remember that mass is measured in kg, there is an incremental gain. A mark or two here is always better than zero marks.

The FIFA method in use (part 2)

In this example, we are using the creative ambiguity inherent in the term “fine tune” rather than “rearrange” to resolve a possible difficulty with unit conversion.

In this example, we resolve another potential difficulty with unit conversion during the our creatively ambiguous “fine tune” stage:

The emphasis, as always, is to resolve issues sequentially and individually in order to minimise cognitive overload.

The FIFA method and low demand Foundation tier calculation questions

I teach the FIFA method to all students, but it’s essential to show how the method can be adapted for low demand Foundation tier questions. (Note: improving student performance on these questions is probably a more significant and quicker and easier win than working on their “extended answer” skills).

For the treatment below, the assumption is that students have already been taught the FIFA method in a number of contexts and that we are teaching them how to apply it to the calculation questions on the foundation tier paper, perhaps as part of an examination skills session.

For the majority of low demand questions, the required formula will be supplied so students will not need to recall it. What they will need, however, is support in inserting the values correctly. Providing a framework as shown below can be very helpful:

Also, clearly indicating where the data came from is useful.

The fine tune stage is not needed, so we can move straight to the answer.

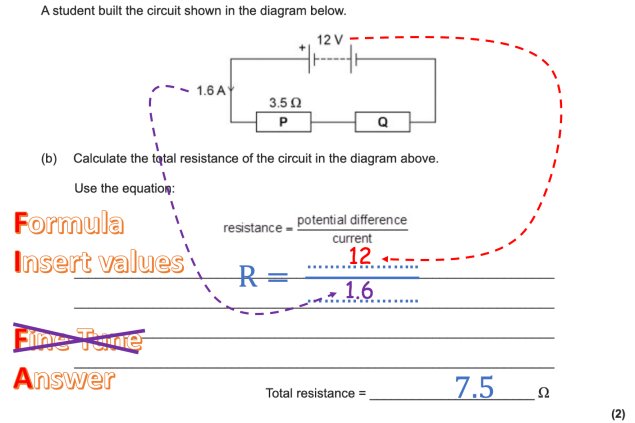
Note also that the FIFA method can be applied to all calculation questions, not just the ones that could be answered using formula triangle methods, as in part (c) of the question above.

And finally…

I believe that using FIFA helps to make our thinking and methods in Physics calculations more explicit and clearer for students.

My hope is that science teachers reading this will give it a go.

You can read about using the FIFA system for more challenging questions by clicking on these links: ‘Physics six mark calculation? Give it the old FIFA-one-two!‘ and ‘Using the FIFA system for really challenging GCSE calculations‘.

PS If you have enjoyed this, you might also enjoy Dual Coding SUVAT Problems and also Magnification using the Singapore Bar Model.

*Disclaimer: AQA has not endorsed the FIFA method. I describe it as “AQA mark scheme-friendly” using my professional own judgment and interpretation of published AQA mark schemes.

Addendum

I am embarrassed to admit that this was the original version published. Somehow I missed the more straightforward way of “fine tuning” by squaring the 30 and multiplying by 0.5 and somehow moved straight to the cross multiplication — D’oh!

My thanks to @BenyohaiPhysics and @AdamWteach for pointing it out to me.